Lewis Number Calculator:
Posted on November 16th, 2020
Lewis Number
The Lewis number is characterized as the proportion of warm diffusivity and mass diffusivity. It is utilized to portray liquid streams where there is synchronous warmth and mass exchange. The Lewis number is subsequently a proportion of the overall warm and focus limit layer thicknesses.
The Lewis number is one of those valuable dimensionless numbers—like the Reynolds number and the Peclet number—that sums up the overall significance of two actual components. Since these numbers are dimensionless, their qualities doesn't rely upon the arrangement of units you use.
The Lewis number is defined as:

where:
α is thermal diffusivity [m2/s]
D is the mass diffusivity [m2/s]
Similarly as for Schmidt and Prandtl Number, the Lewis number physically relates the relative thickness of the thermal layer and mass-transfer (concentration) boundary layer.

where n = 1/3 for most applications in all three relations. These relations, in general, are applicable only for laminar flow and are not applicable to turbulent boundary layers since turbulent mixing in this case may dominate the diffusion processes.
A Lewis number of solidarity shows that warm limit layer and mass exchange by dissemination are similar, and temperature and focus limit layers nearly harmonize with one another. Mass diffusivity or dissemination coefficient is a proportionality consistent between the molar motion because of atomic dispersion and the inclination in the convergence of the species (or the main impetus for dispersion).
Diffusivity is experienced in Fick's law, which states:
In the event that the convergence of a solute in one district is more prominent than in another of an answer, the solute diffuses from the locale of higher focus to the area of lower fixation, with a greatness that is relative to the focus angle.
n one (spatial) dimension, the law is:
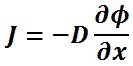
where:
- J is the diffusion flux,
- D is the diffusion coefficient,
- φ (for ideal mixtures) is the concentration.